t-분포를 쉽게 이해하려면,

이 분포는 순전히 평균검정을 하기 위해 고안되었다는 점을 알고 있어야 한다.
 

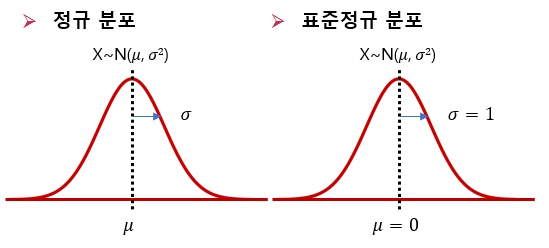
만약 모집단이 정규분포를 따른다고 하면, 표본평균은, 𝐗~𝑵(𝝁, 𝝈^𝟐/𝒏)을 따른다.
그래서 과거에는 이를 이용하여 평균 검정을 해왔는데, 일반적으로 우리는 모분산인 𝝈^𝟐을 알 길이 없다.

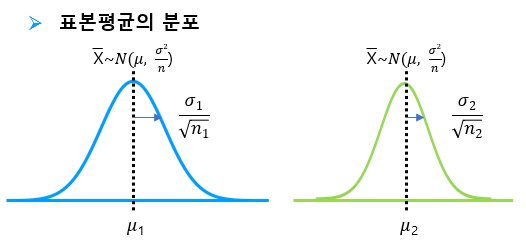
만약 n이 매우 크다면 표본평균은 더욱 정확히 정규분포를 따를 것이고, 표본평균의 분산 역시 0으로 점차 수렴하게 된다. 이 경우, 사실상 𝜎2의 영향이 미미하게 되어 무시할 수 있지만, 표본 수 n이 작을 때는 문제가 될 수 있다. 모분산 𝝈^𝟐을 정확히 알 수 없을 뿐 아니라, 그 값에 따라 정규분포의 모양이 크게 좌지우지되어, 정규분포를 이용한 검정이 그 신뢰성을 잃게되기 때문이다.

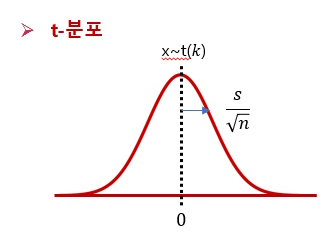
이 경우의 검정을 위해, 정규분포와 형태는 비슷하지만 모분산 항을 포함하고 있지 않고, 대신 표본분산을 이용한 분포를 고안해 내었는데, 그것이 t-분포이다. t분포는 정규분포와 같이 중심을 기준으로 좌우 대칭이고 종모양의 형태를 갖고 중심은 0으로 고정되어 있다.
즉, 표준정규분포와 중심이 같고 자유도(degree of freedom, df)에 따라 종모양의 형태가 조금씩 변한다. df는 표본 수와 관련이 있는 개념으로, 표본(n)이 많아지면 표준정규분포와 거의 동일한 형태를 보인다.

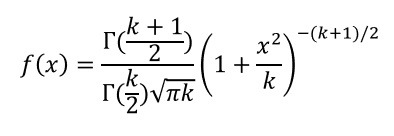
 𝑦~𝑡(𝑘)이면, 확률밀도함수 𝑓(𝑥)는 다음 식으로 표현된다. 여기서, k=자유도,−∞<y<∞

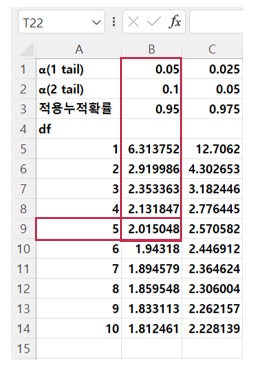
t-분포 테이블에서 예를 들어, 자유도=5의 경우 α값(1 tail)=0.05와 α값(2 tail)=0.1의 적용누적확률이 같은 0.95이며, t-값도 동일하게 2.015일까?


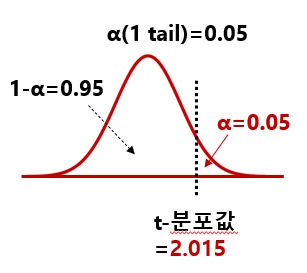
■ 핵심 컨셉: 1) 단측 검정(1 tail): 검정 통계량이 분포의 한쪽 꼬리에 속할 확률을 평가한다. 2) 양측 검정(2 tail) : 검정 통계량이 분포의 양쪽 꼬리에 속할 확률을 평가한다.

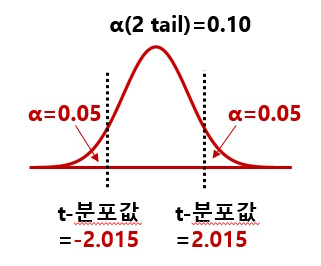
■ 양측 검정(2 tail) 𝛼=0.10: 좌우측 각 𝛼/2=0.05 1) 우측의 누적확률: 1−𝛼=0.95, t-값: T.INV(0.95, 5)=2.015 2) 좌측의 누적확률: 𝛼=0.05, t-값: T.INV(0.05, 5)=-2.015 3) 해석: 좌우의 각 𝛼=0.05에 대한 t-값=±2.015로서 대표값으로 2.015를 사용한다.

t-분포는 모집단이 정규분포를 하더라도 분산(σ²)이 알려져 있지 않고, 표본의 수가 적은 경우에, 평균 μ에 대한 가설검정 및 신뢰구간 추정에 유용하게 사용된다.

t-분포는 모분산을 알 수 없을 때 정규분포 대신 사용한다.
모분산을 알 수 없고, 표본의 크기가 작은 데이터를 검정하려면 t-분포를 사용한다.

■ 가설 검정(t 검정): 𝒕=(𝒙−𝝁)/(𝒔/√𝒏)
일표본 t-검정(1 Sample t-test): 모집단의 평균이 특정값이라고 할 수 있는가를 검정할 때 사용한다
이표본 t-검정(2 Sample t-test): 두 모집단의 평균이 다르다고 할 수 있는 가를 검정할 때 사용한다
대응표본 t-검정(Paired Sample t-test): 모집단의 짝지어진 변수들의 평균이 다르다고 할 수 있는 가를 검정할 때 사용한다

■ 신뢰 구간, μ의 100(1-a)% 신뢰구간: