
때때로 로지스틱/프로빗 회귀분석을 실행할 때 소위 완전분리 또는 준완전분리 문제가 발생한다.
여기에서 사용된 예제 데이터 세트는 매우 작은 경우이며 설명의 목적으로만 사용된다.
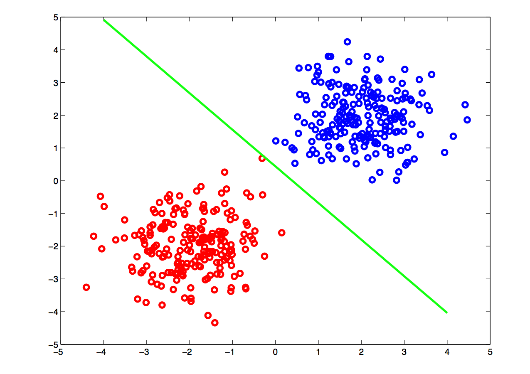
완전한 분리는 반응변수가 예측변수 또는 예측변수 조합을 완전히 분리할 때 발생한다.
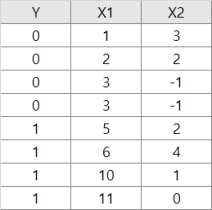
이 예에서 Y는 반응변수이고 X1과 X2는 예측변수이다.
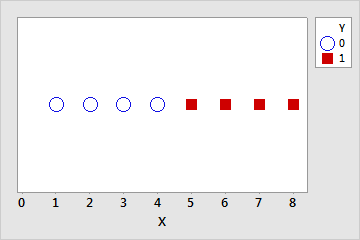
Y = 0인 관측치는 모두 X1<=3의 값을 갖고 Y = 1인 관측치는 모두 X1>3의 값을 가짐을 알 수 있다.
즉, Y는 X1을 완벽하게 분리한다.
다른 방법은 X1<=3이 Y = 0에 해당하고 X1>3이 Y = 1에 해당하기 때문에
X1이 Y를 완벽하게 예측한다는 것이다.
완전한 분리 또는 완벽한 예측은 여러가지 이유로 발생할 수 있다.
한 가지 일반적인 예는 범주가 지표로 코딩된 여러 범주형 변수를 사용할 때이다.
예를 들어, 연령 관련 질병(현재/없음)을 연구하고 있고 연령이 예측 변수 중 하나인 경우
해당 질병이 있는 하위 그룹(예: 55세 이상의 여성)이 있을 수 있다.
코딩 오류가 있거나 다른 버전의 결과를 예측 변수로 잘못 포함시킨 경우에도
완전한 분리가 발생할 수 있다.
예를들어, 연속변수 X를 이진 변수 Y로 이분법화 했을 수 있다.
그런 다음 Y와 일부 예측변수 간의 관계를 연구하고 싶었다.
X를 예측변수로 포함하면 정의에 따라 Y가 X를 완전히 분리하기 때문에
완벽한 예측의 문제에 직면하게 된다.
완전한 분리가 일어날 수 있는 다른 시나리오는 표본 크기가 매우 작은 경우이다.
위의 예제 데이터에서 X1이 <=3일 때 Y가 0이어야 하는 이유는 없다.
표본이 충분히 크면 Y = 1 및 X1 <=3인 일부 관측값이 있어 X1의 완전한 분리를 깨뜨릴 수 있다.
X1과 X2에 Y의 로지스틱 또는 프로빗 회귀 모델을 맞추려고 하면 어떻게 될까?
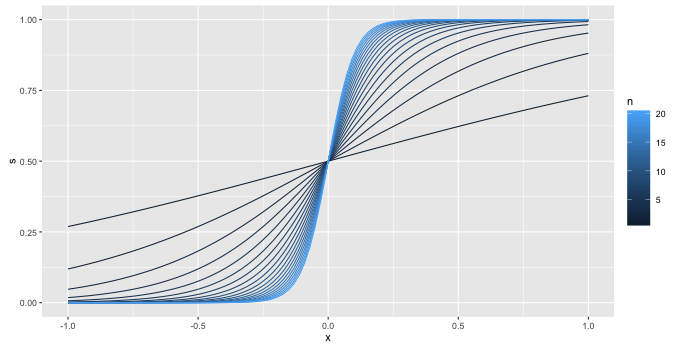
수학적으로 X1에 대한 최대우도 추정치는 존재하지 않는다.
특히 이 예에서 X1에 대한 계수가 클수록 가능성이 커진다.
즉, X1에 대한 계수는 가능한 한 커야 하며, 이는 무한대이다!
[계속]
