이제 Bayesian의 위력을 가장 잘 실감할 수 있는 예가 등장한다. 바로 Credible interval이다.
Credible interval의 개념 자체는 일반적인 신뢰구간과 거의 비슷하다. 하지만 그 해석은 완전히 반대이다.

결론부터 말하자면, Credible interval 이야말로 연구자들이 진실로 원하는 결과를 가져다 주지만,

현실은 그렇게 해 주지 못하는 신뢰구간(Confidential interval)이 압도적으로 많이 사용되고 있다.

보통 사람들은 데이터를 모은 뒤에,
내가 세운 가설이 데이터에 비추어보았을 때 얼마나 그럴듯한지, 아닌지에 관심이 많다.
다시 말해 사람들이 진정으로 원하는 것은 p(θ|Data) 수식의 값이다.

위 확률은 데이터를 관측한 뒤, 모수치가 어떤 값을 가질 확률을 의미한다. 그런데 당연하게도 이 확률은
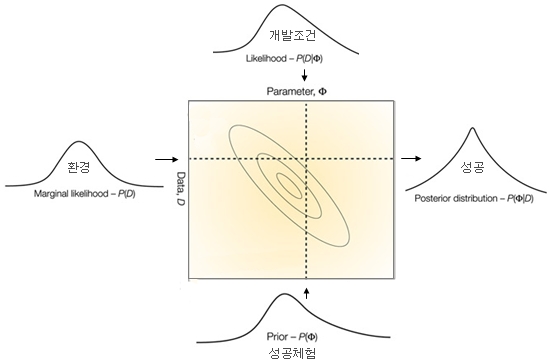
베이즈정리에 의해 p(θ|Data) = p(Data|θ)* p(θ) / p(Data) 로 표현할 수 있다. 이 식은 모수치에 대해 사전에
갖고 있던 믿음인 p(θ)가 데이터에 의해 어떻게 p(θ|data)로 업데이트 되는지를 나타낸다.
따라서 자연스럽게 베이즈정리를 이용하여 믿음을 업데이트하기만 하면 되지 않을까?

그런데 사실, 일반적으로 많이 사용하는 통계학에서는 위의 식은 의미가 없다. 사용해서는 절대 안 되는 식이다.
왜 그럴까? 바로 빈도주의 통계학에서 모수치인 θ는 'fixed but unknown constant' 이기 때문이다.
누가 감히 신성한 constant에다가 '확률'따위를 부여할 수 있다는 말인가?

잘 모르긴 하지만, 아마도 모수치는 분명히 고정된 상수일 것이다, 바로 이것이 빈도주의 통계의 기본 가정이다.
아마 신뢰구간의 해석에 대해 배울 때, 이상한 말을 많이 들었을 것이다. 이를테면 다음과 같은 것이다.

 "95% 신뢰구간을 해석할 때, 95%라는 확률을 절대로 'θ가 신뢰구간 안에 있을 확률' 로 해석하지 말고,
 '신뢰구간을 아주 많이 만들었을 때 그 신뢰구간이 θ를 포함할 확률'로 해석할 것."

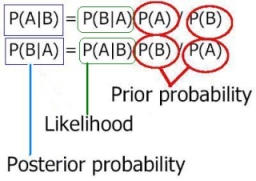
대체 이게 무슨 소린가? 바구니를 옮겨서 사과를 담으나,

사과가 바구니 안으로 떨어지나, 비슷한 소리 아닌가?
하지만 빈도주의 통계에서는 "사과가 떨어질 곳은 정해져 있는데, 우리가 모를 뿐이다.

바구니를 굉장히 많이 옮겨 보면 한 95% 정도는 우리가 바구니를 놓은 곳에

사과가 떨어질 것이다!" 라고 이야기한다는 것이다.

그런데 여기서 중요한 것은, '굉장히 많이'라는 말이다.

결국 빈도주의 통계입장에서는 단 하나의 신뢰구간을 계산하면,
 'θ가 이 구간 안에 들어있거나, 들어있지 않거나, 둘 중 하나이다.

즉 확률은 0 이거나 1이다.'

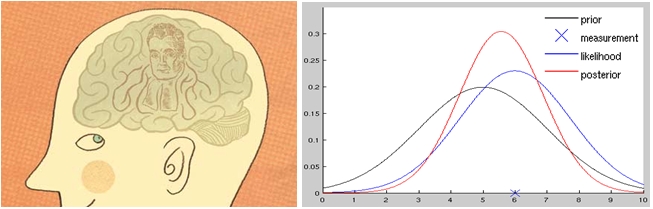
베이지안 통계에서는 θ도 확률변수로 취급하기 때문에

θ는 더이상 베일에 가져려 있는 신비한 존재가 아니다.
따라서 '이 신뢰구간(베이지안 용어로 CREDIBLE INTERVAL이다.)안에 θ가 들어있을 확률이 95%이다.'

따위의 진술을 하여도 전혀 이상할 것이 없다.

그리고 우리는 애초에 원했던 결과, 즉 P(θ|Data)를 얻을 수 있다.

사실 직관적으로 보았을 때, 이러한 것이 당연한 것임에도 불구하고,

고전통계의 절차들은 대단히 자주 남용되고 있으며, 오해석되고 있는 것이 현실이다.

베이지안통계는 이러한 현실을 개선하는 데도 큰 도움을 줄 수 있으리라 생각한다.